• Les géométries non euclidiennes
  D'Euclide à Poincaré, la saga des figures étranges
  introduction
  Les travaux de Lobatchewsky
  La géométrie analytique non euclidienne
  Le point de vue moderne
  Le point de vue contemporain
  Bibliographie
• Volume de l'hypersphère
  pourquoi les banquiers n'ont pas de lingots sphériques
  
• L'axiome du choix
  polémiques et paradoxes
  
• Fonctions continues sans dérivées
  les monstres qui effrayaient Charles Heremite
• Le nombre pi
  décimales et algorithmes
  
• 1+2+3+... = -1/12
  vu dans "Ciel et Espace" N0 238 page 32
  
• La logique formelle
  les formalismes des fondemants des mathématiques
  
• Termes inversibles en Lambda calcul
  mémoire de DEA
  
• Mathématiques pour un anniversaire
  curieuses formules
  
• Mes bouquins de maths préférés
  de saines lectures pour les soirées d'hiver
  
• Liens et autres sites
  un petit tour chez les collègues
  

Considérons maintenant un ensemble d'horocycles associées à un même faisceau de parallèles comme sur la figure 8.

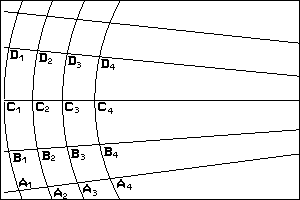Figure 8

Chisissons ces horocycles tels que A₁A₂ = A₂A₃ = A₃A₄, alors par propriété des horocycles on a A₁A₂ = B₁B₂ = C₁C₂ = B₂B₃ = ... et si de plus on a A₁B₁ = B₁C₁ = C₁D₁ alors A₂B₂ = B₂C₂ = C₂D₂ c'est la propriété euclidienne des horocycles. Naturellement la distance A₁B₁ est prise sur l'arc d'horocycle. Les longueurs A₁B₁, A₂B₂, A₃B₃ décroissent et ceci proportionnellement aux distances A₁A₂, A₂A₃ et l'on a A₁B₁/A₂B₂ = B₁C₁/B₂C₂ = C₁D₁/C₂D₂.
Appelons x et y les distances respectives A₁A₂ et A₂A₃ (A₁A₂ = x, A₂A₃ = y). Ainsi A₂B₂ ne dépend que de A₁B₁ et de x et nous avons: A₂B₂/A₁B₁ = f(x) et A₃B₃/A₂B₂ = f(y), mais on a aussi A₃B₃/A₁B₁ = f(x+y). Mais on peut écrire: A₃B₃/A₁B₁ = (A₃B₃/A₂B₂).(A₂B₂/A₁B₁) = f(x).f(y) . On a donc en définitive f(x+y) = f(x).f(y) et l'on voit ainsi apparaître mystérieusement la fonction exponentielle.
Nous pouvons exploiter ce résultat:

f(0+0) = f(0).f(0) = f(0)
f(0)[f(0) - 1]=0 ce qui implique f(0) = 0 ou f(0) = 1

f(0) = 0 n'est pas possible car on aurait alors la fonction nulle ce qui fait disparaître la géométrie. Il reste donc f(0) = 1.
De même f(1 + 1) = f(1).f(1) = [f(1)]² = f(2) si nous posons: f(1) = a, nous avons f(2) = a², f(n) = a^n et de manière plus générale f(p/q) = a^(p/q) et enfin si nous admettons la continuité de l'espace: f(x) = a^x pour x réel, ce qui peut s'écrire aussi f(x) = exp(x.log(a)).

Une question se pose maintenant, quelle est la valeur de a ?
Sur notre figure nous avons choisi A₂B₂ < A₁B₁ ce qui nous conduit à 0 < a < 1

La valeur a = 1 nous conduit à la géométrie euclidienne. mais en géométrie non euclidienne cette valeur n'est déterminée que par l'inégalité précédente. Ainsi dans cette géométrie apparait une constante arbitraire. Nous avons donc log(a) < 0, posons k' = -log(a) ce qui nous donne une constante positive. De plus on pose k= 1/k', k jouant ainsi le rôle du rayon de courbure de l'espace de Labatchevsky, et donc f(x) = exp(-x/k).

Pour revenir à la figure 8 nous avons donc:

A2B2 = A1B1.exp(-A1A2/k)

A1B1 = A2B2.exp(A1A2/k)

La fonction P(x) de Labatchevsky

Dans le chapitre précédent nous avons rapidement vu que l'angle limite de Labatchevsky est une fonction décroissante de la distance du point de l'angle à la parallèle. Examinons la figure 9

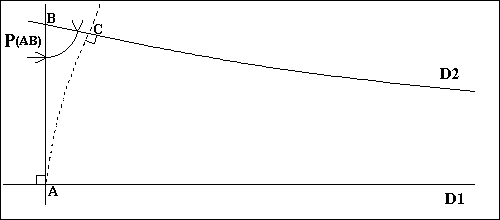Figure 9

nous y voyons une droite D₁, un point B , sa projetction sur D₁ en A et la parallèle D₂ à D₁ passant par B . Nous avons aussi dessiné en pointillé l'horocycle d'axe D₁ passant par A et coupant D₂ en C .
Nous savons que l'angle ABC est inférieure à 90 degrés et qu'il dépend de la distance AB . Labatchevsky note P(AB) cet angle. Son évaluation est un peu délicate, on en trouvera le détail dans ....... cependant on montre que:

sin(P(AB)) = exp(-BC/k)

et surtout, en posant AB = x pour simplifier les écritures:

P(x) = 2arctg(exp(-x/k))

tg(P(x)/2) = exp(-x/k)

On constate immédiatement que:

• quand B se rapproche de A , AB tend vers 0 et langle tend vers 2arctg(1) = 90 degrés.
• si k tend vers l'infini (rayon de courbure de l'espace infini) alors l'angle ne dépend plus de la distance AB et il est constant valant alors 90 degrés. C'est la géométrie euclidienne, celle-ci apparaît comme un cas particulier de géométrie non euclidienne.

Trigonométrie du triangle rectangle

Il est bien sur possible d'exprimer les fonctions circulaires de cet angle. En utilisant les formules bien connues

cos(a) = [1 - (tg(a/2))²]/[1 + (tg(a/2))²]
sin(a) = 2tg(a/2)/[1 + (tg(a/2))²]
tg(a) = 2tg(a/2)/[1 - (tg(a/2))²]

et en remplaçant a par P(x) on obtient:

cos(P(x)) = [1 - 2exp(-x/k)]/[1 + 2exp(-x/k)] = th(x/k) (1)
sin(P(x)) = 2exp(-x/k)/[1 + 2exp(-x/k)] = 1/ch(x/k) (2)
tg(P(x)) = 2exp(-x/k)/[1 - 2exp(-x/k)] = 1/sh(x/k) (3)

Lobatchevsky applique ces résultats au triangle rectangle. Examinons la figure 10:

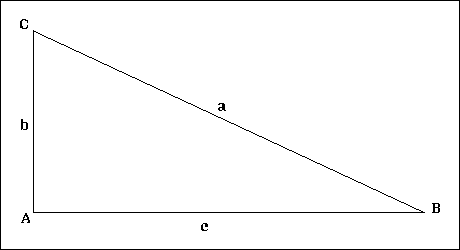Figure 10

Nous y voyons un triangle rectangle ABC dont les cotés mesurent a,b,c

On établit alors les relations suivantes dans le triangle rectangle:

cos(C) = th(b/k) / th(a/k)
sin(C) = sh(c/k) / sh(a/k)
tg(C) = th(c/k) / th(b/k)

cos(B) = th(c/k) / th(a/k)
sin(B) = sh(b/k) / sh(a/k)
tg(B) = th(b/k) / th(c/k)

En utilisant ces formules et en égalant les valeurs de tg(B) et de sin(B)/cos(B) calculées de deux manières différentes on aboutit à la relation suivante entre les trois cotés d'un triangle rectangle:

ch(a/k) = ch(b/k).ch(c/k) (4)

On peut aussi écrire:

1/ch(a/k) = 1/ch(b/k) . 1/ch(c/k)

Et en appliquant la formule (2) on obtient

sin(P(a)) = sin(P(b)) . sin(P(c))

On peut trouver ansi un grand nombre de formules analogues caractérisant la trigonométrie de la géométrie de Lobatchevsky. On les trouvera dans l'article de Lobatchevsky "Géométrie imaginaire".

La formule (4) ci-dessus est remarquable, elle représente l'équivalent du théorème de Pythagore pour la géométrie euclidienne. On peut le voir en faisant un développement limité à l'ordre 2 de ch(x/k) = 1 + (x²)/(2k²) nous obtenons

1 + (a²)/(2k²) = (1 + (b²)/(2k²)) . (1 + (c²)/(2k²))
1 + (a²)/(2k²) = 1 + (b²)/(2k²) + (c²)/(2k²) + (b².c²)/(4k^4)

Le dernier teme est d'ordre 4, on le néglige et nous obtenons

1 + (a²)/(2k²) = 1 + (b²)/(2k²) + (c²)/(2k²)
(a²)/(2k²) = (b²)/(2k²) + (c²)/(2k²)
a² = b² + c²

C'est-à-dire le théorème de Pythagore de la géométrie euclidienne. Ce petit calcul montre que la géométrie euclidienne est la géométrie limite de celle de Lobatchevsky pour des petites distances. On obtient un résultat analogue si l'on fait tendre la courbure de l'espace k vers l'infini, ce qui montre que la géométrie euclidienne est une géométrie non euclidienne de rayon de courbure infini, c'est-à-dire un espace plat. La géométrie de Lobatchevsky est une géométrie plus générale.

Lobatchevsky développe ensuite la trigonométrie pour les triangles quelconque. Il établit que l'aire d'un triangle n'est autre que son déficit. Donnons pour terminer ce chapitre les valeurs du périmètre du cercle ainsi que son aire.

aire du cercle de rayon r

2.Π.k²(ch(r/k) - 1) = 4.Π.k².(sh(r/2k))²
= Π.k²(exp(r/2k) - exp(-r/2k))²

périmètre du cercle de rayon r

2.Π.k.sh(r/k)

Volume de la sphère de rayon r

Π.k³(sh(2r/k) - 2r/k)

aire de la sphère de rayon r

4.Π.k²(sh(r/k))²

On laisse le soin au lecteur de montrer qu'en faisant tendre k vers l'infini on retrouve les valeurs connues de la géométrie euclidienne.

Le point de vue moderne