Une méthode simple
Pour le savoir simplement nous allons comparer la distribution des décimales de PI en base 2 avec le jet aléatoire d'une pièce de monnaie.
Pour cela nous allons définir deux variables aléatoires X1 et X2. X1 est associée au jet d'une pièce de monnaie et prend ses valeurs dans l'ensemble {0,1,...,n} et représente combien de fois la face pile est sortie après avoir lancé n fois la pièce. La variable aléatoire X2 représentera le nombre de décimales valant 1 dans le développement de PI en base 2 jusqu'à n décimales.
La première variable aléatoire est théorique, la loi de probabilité associée est bien connue. La seconde (X2) est empirique, les décimales de PI sont déterminées depuis longtemps, ce que l'on ne connait pas à priori est sa loi de probalité qu'il va falloir déterminer par le calcul. Si on s'aperçoit alors qu'elle est proche de celle de X1 on pourra conclure que les décimales de PI sont presqu'aussi aléatoires que le jet d'une pièce de monnaie.
La variable aléatoire X1 suit une loi binomiale de moyenne np et de variance npq avec n nombre de tirage, p probabilité d'avoir 1 et q probabilité d'avoir 0. Ici on a p = q = 0.5.
Dans le tableau ci-dessous on compare les deux variables aléatoires sur une variété d'intervalles de la suite des décimales en base 2.
| INTERVALLE | NB 0 | NB 1 | PROBABILITE | MOYENNE | VARIANCE | |||
|---|---|---|---|---|---|---|---|---|
| | | | X2 | X1 | X2 | X1 | X2 | X1 |
| 1 -100000 | 50077 | 49923 | 0.5008 | 0.5 | 50076.99728 | 50000.000 | 24999.94071 | 25000.000 |
| 1 -300000 | 149891 | 150109 | 0.4996 | 0.5 | 149891.00397 | 150000.000 | 74999.96040 | 75000.000 |
| 1 -500000 | 249651 | 250349 | 0.4993 | 0.5 | 249650.99990 | 250000.000 | 124999.75640 | 125000.000 |
| 1 -750000 | 374715 | 375285 | 0.4996 | 0.5 | 374714.99294 | 375000.000 | 187499.89169 | 187500.000 |
| 1 -1000000 | 499721 | 500279 | 0.4997 | 0.5 | 499720.99066 | 500000.000 | 249999.92215 | 250000.000 |
| 100000-200000 | 50027 | 49974 | 0.5003 | 0.5 | 50027.00049 | 50000.500 | 25000.24298 | 25000.250 |
| 200000-300000 | 49788 | 50213 | 0.4979 | 0.5 | 49788.00136 | 50000.500 | 24999.79845 | 25000.250 |
| 300000-400000 | 49660 | 50341 | 0.4966 | 0.5 | 49659.99910 | 50000.500 | 24999.09060 | 25000.250 |
| 400000-500000 | 50101 | 49900 | 0.5010 | 0.5 | 50101.00040 | 50000.500 | 25000.14900 | 25000.250 |
| 500000-600000 | 50165 | 49836 | 0.5016 | 0.5 | 50164.99854 | 50000.500 | 24999.97940 | 25000.250 |
| 600000-700000 | 49804 | 50197 | 0.4980 | 0.5 | 49803.99940 | 50000.500 | 24999.86388 | 25000.250 |
| 700000-800000 | 50201 | 49800 | 0.5020 | 0.5 | 50201.00011 | 50000.500 | 24999.84800 | 25000.250 |
| 800000-900000 | 49915 | 50086 | 0.4991 | 0.5 | 49914.99926 | 50000.500 | 25000.17690 | 25000.250 |
| 900000-1000000 | 49987 | 50014 | 0.4999 | 0.5 | 49986.99941 | 50000.500 | 25000.24818 | 25000.250 |
On constate une bonne coincidence. Bien sur il faudrait multiplier les intervalles de mesure pour se faire une idée plus précise.
Une méthode plus fine.
Un méthode un peu plus complexe consiste à prendre les décimales de pi par bloc de n chiffres, de considerer le nombre P formé par les n chiffres et de le diviser par 10n. On fabrique ainsi un nombre compris dans l'intervalle [0,1[ à l'aide des décimales de pi. En répétant l'opération Q fois on obtient une suite de nombres de [0,1[. Si cette suite est aléatoire, on peut admettre que les chiffres qui les composent sont aussi aléatoires.
Ici nous allons prendre comme référence, non pas une loi
binomiale comme précédemment, mais une variable aléatoire
uniforme sur [0,1].
Soit X une variable aléatoire uniforme sur [0,1] et X1 la variable
aléatoire associée aux nombres obtenus. La moyenne et la variance
de X sont connus, elles valent respectivement 1/2 = 0.5 et 1/12 = 0.08333...
Nous allons pour des valeurs variées de n et de Q calculer sur les décimales de pi en base 10 la moyenne et la variance des Q nombres ainsi obtenus et de les comparer aux valeurs théoriques 0.5 et 0.08333..
| n | Nb de nombres | Décimales concernées | Moyenne | Variance |
|---|---|---|---|---|
| 1 | 362 880 | 362 880 | 0.449939 | 0.082492 |
| 2 | 181 400 | 362 880 | 0.493929 | 0.083167 |
| 3 | 120 933 | 362 880 | 0.499686 | 0.083260 |
| 4 | 90 700 | 362 880 | 0.498982 | 0.083177 |
| 5 | 72 560 | 362 880 | 0.499953 | 0.083336 |
| 6 | 60 466 | 362 880 | 0.498640 | 0.083329 |
| 7 | 51 828 | 362 880 | 0.495155 | 0.082651 |
| 8 | 45 350 | 362 880 | 0.497753 | 0.083349 |
| 9 | 40 311 | 362 880 | 0.501186 | 0.083458 |
| 6 | 70 000 | 420 000 | 0.498845 | 0.083327 |
| 6 | 80 000 | 480 000 | 0.499514 | 0.083498 |
| 5 | 100 000 | 500 000 | 0.498637 | 0.083275 |
| 4 | 125 000 | 500 000 | 0.499440 | 0.083328 |
TOUJOUR PLUS FORT: Le calcul de pi à partir de ses décimales.
A partir d'une suite de nombres aléatoires de l'intervalle [0,1[, il est possible de calculer une approximation de pi par la méthode de Monte Carlo.Soit en effet un carré de coté 1 ABCD et le cercle de rayon 1 de centre A comme sur la figure ici:
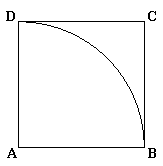
L'aire du quart de cercle est pi/4. Le rapport de l'aire du quart de cercle à celle du carré est aussi pi/4.
Si nous notons n(i) l'ensemble des Q nombres de [0,1[, et Q pair, alors on peut
considérer les couple ( n(i), n(i+Q/2) ). Si ces couples de points sont
répartis au hasard ils occupent le carré uniformément et
la proportion de ceux qui occupent le quart de cercle donnent une approximation
de pi/4.
Choisissons les valeurs de la ligne 5 du
tableau ci-dessus qui donne les meilleurs résultats. Nous obtenons:
n = 5; nombre de points: 72 560/2 = 36 280; nombre de points dans le quart de
cercle:28 518
alors 28 518/36 280 = 0.786052921719 et pi = 4*0.786052921719 = 3.144211686876
On trouvera d'autres méthodes plus sophistiquées dans [BOY 1].
