• Les géométries non euclidiennes
  D'Euclide à Poincaré, la saga des figures étranges
  introduction
  Les travaux de Lobatchewsky
  La géométrie analytique non euclidienne
  Le point de vue moderne
  Le point de vue contemporain
  Bibliographie
• Volume de l'hypersphère
  pourquoi les banquiers n'ont pas de lingots sphériques
  
• L'axiome du choix
  polémiques et paradoxes
  
• Fonctions continues sans dérivées
  les monstres qui effrayaient Charles Heremite
• Le nombre pi
  décimales et algorithmes
  
• 1+2+3+... = -1/12
  vu dans "Ciel et Espace" N0 238 page 32
  
• La logique formelle
  les formalismes des fondemants des mathématiques
  
• Termes inversibles en Lambda calcul
  mémoire de DEA
  
• Mathématiques pour un anniversaire
  curieuses formules
  
• Mes bouquins de maths préférés
  de saines lectures pour les soirées d'hiver
  
• Liens et autres sites
  un petit tour chez les collègues
  

Les géométries non euclidiennes ont joué un rôle très important dans l'histoire de la géométrie et son élaboration. Aujourd'hui ces théories sont achevées et elles sont présentées comme la géométrie d'une forme bilinéaire symétrique de signature (1,n - 1) dans un espace projectif de dimension n. Cette vision très synthétique a l'inconvénient de masquer toute la démarche historique qui a conduit à leur achèvement.
On trouvera dans l'exposé qui suit une présentation générale de ces géométries depuis l'antiquité jusqu'aux théories modernes. Nous nous contenterons d'un survol ne donnant que les démonstrations les plus simples ainsi que les principaux résultats. La bibliographie abondante permettra au lecteur tous les approfondissements nécessaires.

Un peu d'histoire (introduction)

L'histoire des géométries non-euclidiennes commence avec l'antiquité et les travaux d'Euclide sur la formalisation de la géométrie.

Euclide, au 3ème siècle avant Jésus-Christ pose les premiers fondement de la géométrie. Dans son oeuvre il construit la géométrie en posant des définitions (35 pour le premier livre), des postulats (6) qu'il nomme demandes et des axiomes (9) qu'il nomme notions communes.

Les définitions sont relatives au point, à la droite, au plan, au cercle, au triangle, au paraléllogramme etc.... qui sont ainsi caractérisés.

Les postulats sont des possibilités de construction admises comme par exemple

Conduire une droite d'un point quelconque à un point quelconque

ou bien

prolonger indéfiniment, selon sa direction une droite finie

Les axiomes sont des généralités admises sur la l'utilisation des concepts mathématiques comme

Les grandeurs égales à une même grandeur sont égales entr'elles

A l'aide de ces données Euclide fonde la géométrie et montre l'existence de triangles (isocèles, équilatéraux), les cas d'égalité des triangles, la possibilité de diviser les angles, l'unicité de la perpendiculaire à une droite en un point etc...

Le problème apparait avec le 5ème postulat, dit postulat des parallèles et qu'Euclide formule ainsi:

Si une droite, tombant sur deux droites, fait les angles intérieurs du même coté plus petits que deux droits, ces droites prolongées à l'infini se rencontreront du coté où les angles sont plus petits que deux droits.

Ce postulat parait compliqué et tellement évident que l'on s'est demandé s'il était bien nécessaire. On n'en a pas besoin pour démontrer l'existence des parallèles, il n'intervient seulement pour démontrer l'unicité d'une parallèle à une droite passant par un point donné.

Depuis l'antiquité on a essayé de démontrer ce postulat. Certains ont cru y être parvenus. Des Grecs aux Arabes en passant par les Italiens au XVIème siècle un grand nombre de savants se succèdent sur ce problème. Quelques uns obtiennent des résultats tout à fait intéressants. Citon Saccheri (1667 - 1673) qui en prenant un raisonnement par l'absurde ira très loin dans la construction d'une géométrie à plusieurs parallèles en utilisant un quadrilatère à deux angles droits et deux cotés égaux, mais il finit par rejeter l'ensemble aux pretextes que les résultats lui paraissent bizarres et ne pas conrrespondre à la réalité. Peu après lui Lambert (1728 - 1777) reprend un raisonnement analogue mais avec un quadrilatère à trois angles droits, et va aussi très loin dans le développement de la nouvelle géométrie mais n'arrive pas à se convaincre que la géométrie obtenue est autonome. Il est vrai qu'à l'époque la distinction entre géométrie physique et géométrie mathématique n'avait pas de sens. La géométrie devait d'une certaine manière représenter le réel.

Legendre à son tour au début du XIXème siècle s'attaque au problème et donne dans ses ouvrages plusieurs démonstration de ce postulat. Démonstrations fausses bien entendu. Il reconnaitra plus tard que sa façon de voir pose des difficultés. Il est intéressant de l'examiner un peu car elle conduit aux fondements de la géométrie non euclidienne. Legendre montre l'équivalence de ce postulat avec la propriété ci-dessous qui servira de base à la construction des géométries non-euclidiennes. Legendre s'est approché de près de la construction de la géométrie non euclidienne, mais son idée était de montrer le postulat des paralèlles. L'examen de la démonstration fausse de Legendre va nous permettre de rentrer de plain pied dans la nouvelle géométrie.

Les travaux de Legendre

Legendre établit d'abord le résultat suivant qui jouera par la suite un rôle important.

Si la somme des angles d'un triangle est égale à 180 degrés (deux droits) alors le 5ème postulat est vrai et réciproquement.

Legendre démontre d'abord que la somme des angles d'un triangle ne peut pas être supérieure à 180 degrés Sa démonstration est rigoureuse et n'utilise pas le postulat de parallèles .

Ensuite il essaie de démontrer que la somme des angles d'un triangle ne peut pas être inférieure à 180 degrés. Regardons un peu sa démonstration.

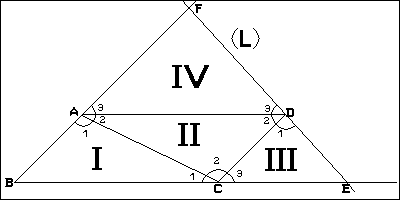Figure 1

Soit un triangle ABC ( figure 1) dont on suppose que la somme des angles est inférieure à 180 degrés soit: 180 - a (a > 0). Construisons le point D symétrique de B par rapport au coté AC, et par ce point D traçons une droite (L) qui coupe le coté AB au point F et le coté BC au point E. Nous obtenons le triangle BFE dont on va essayer de calculer la sommes des angles.

Notons I le triangle ABC, II le triangle ACD, III le triangle CDE et IV le triangle ADF.

Nous savons que la sommes des angles des triangles I et II est 180 - a, mais nous ne connaissons pas la sommes des angles des triangles III et IV. Tout ce que nous savons est que la somme de leurs angles est inférieure ou égale à 180 degrés. Suposons au pire que cette somme soit 180 degrés, sous cette hypothèse la somme des angles de ces quatre triangles vaut:

(180 - a) + (180 - a) + 180 + 180 = 720 - 2a

soit en notant E l'angle Ê pour simplifier

B + E + F + (A1 + A2 + A3) + (C1 + C2 + C3) + (D1 + D2 + D3) = B + E + F + 3*180

d'où

B + E + F = 720 - 2a - 540 = 180 - 2a

Ainsi la somme des angles du grand triangle BEF est inférieure ou égale à 180 - 2a degrés.

Legendre en conclu qu'en construisant un triangle BGH à partir du triangle BEF suivant la même construction on aura la somme des angles du nouveau triangle BGH inférieure ou égale à 180 - 4a degrés et qu'en continuant ainsi on obtiendra un triangle dont les angles sont devenus négatifs ce qui n'est pas possible.

Il est assez difficile pour quelqu'un de très familier avec la géométrie euclidienne de voir l'erreur de raisonnement de Legendre.

En fait Legendre admet dans ce raisonnement implicitement le postulat dit des parallèles quand il fabrique le grand triangle BEF en traçant la droite (L) par D. En effet qu'est-ce qui lui assure qu'à un moment de sa construction la droite (L) n'est pas parallèle à un des deux cotés du triangle d'origine ?
L'existence des points E et F doit être démontrée au cours de cette construction. Et c'est précisément ce qui se passe dans cette nouvelle géométrie, au delà d'une certaine distance du point B la droite (L) est parallèle soit au coté AB, soit au coté BC, soit aux deux coté à la fois et ainsi la construction de Legendre ne peut pas continuer indéfiniment.

Si on admet l'hypothèse que la somme des angles d'un triangle est inférieure à 180 degrés alors appelons S(ABC) la somme des angles du triangle (ABC), et déficit le nombre 180 - S(ABC), noté d(ABC).

Examinons la figure 2:

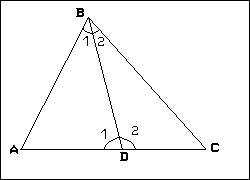Figure 2

Notons d(ABC), d(ABD) et d(BDC) les déficits respectifs des triangles (ABC), (ABD) et (BDC).
Nous avons:

d(ABD) = 180 - S(ABD) et d(BDC) = 180 - S(DBC)
d'où
d(ABD) + d(BDC) = 360 - [S(ABD) + S(DBC)]
or
S(ABD) = A + D1 + B1 et S(DBC) = D2 + B2 + C
et ainsi
S(ABD) + S(DBC) = A + C + (B1 + B2) + (D1 + D2) = A + C + B + 180
d'où
S(ABD) + S(DBC) = S(ABC) + 180
et donc
d(ABD) + d(BDC) = 360 - (S(ABC) + 180) = 180 - S(ABC) = d(ABC)

En conclusion: Le déficit d'un triangle est la somme des déficits des triangles qui le composent. Cela fonctionne comme la mesure des surfaces d'où l'idée de mesurer les surfaces en comptant les déficits.

Le fait pour un triangle de posséder un déficit non nul est caractéristique de la géométrie non euclidienne. On montre en effet que si un seul triangle a un déficit nul alors tous les triangles ont déficit nul et la géométrie est euclidienne.

Réciproquement si un triangle a un déficit non nul alors tous les triangles ont un déficit non nul.

L'existence de triangles à un, deux ou trois angles nuls dans cette géométrie n'est pas la moindre étrangeté que l'on va rencontrer au cours de cette étude. Le lecteur qui se sentirait troublé par cette remarque ne devrait pas poursuivre plus avant sa lecture.

Il existe donc une limite à la construction des triangles dont le fameux triangle à trois angles nuls représente celui qui a la plus grande surface. On en déduit l'impossibilité de paver le plan par des triangles. On obtient le premier résultat important en géométrie non euclidienne:

Le fait que la somme des angles d'un triangle diminue quand sa surface augmente conduit à l'impossibilité d'obtenir des triangles proportionnels et ainsi il existe un quatrième cas d'égalité des triangles exprimé par:

Il n'y a pas de similitude dans cette géométrie.

Les travaux de Lobatchevsky