Mail/M'écrire


Les fonctions continues sans dérivées
(André Brouty Mars 1996)
Cet exposé est sous licence libre LLDD.

  Introduction

Au 18ème siècle la notion de fonction se confondait avec celle de courbe algébrique. Dans l'Encyclopédie de Diderot, à l'article fonction rédigé par D'Alembert on peut lire:
"...... On appelle fonction de x ou en général d'une quantité quelconque, une quantité algébrique composée de tant de termes que l'on voudra et dans laquelle x se trouve de manière quelconque, mélée ou non avec des constantes.Ainsi x2 + x3, √a.a + .x.x, √a.a + x3/b.b + x4, ∫dx√a2 − x2 sont des fonctions de x."
Nous sommes loin de la définition moderne.
Il était à cette époque, intuitif, même évident qu'une fonction continue admette des dérivées, à part quelques points singuliers. Cela paraissait même une vérité première qu'il était inutile de démontrer, puisqu'on pouvait tracer une tangente à la courbe qui la représentait.
Cette notion va se préciser au XIXème siècle avec les travaux de Cauchy, Dirichlet, Riemann et quelques autres. C'est à Riemann que nous devons la définition de fonction telle que nous la connaissons aujourd'hui.
Au début du XIXème siècle les seules fonctions qui présentaient aux yeux des mathématiciens un intérêt certain étaient les fonctions analytiques.
Après 1850 on s'intéresse à l'étude des séries trigonométriques qui jouent un rôle important en physique où elles interviennent dans l'équation des cordes vibrantes et dans les séries de Fourier.
Il est facile de voir qu'une fonction dérivable en tout point d'un domaine y est continue. La réciproque est fausse. Les contre-exemples abondent.

  Les travaux de Weierstrass

Weierstrass (1815 - 1897) fut le premier à donner en 1861 un exemple de fonction continue n'admettant de dérivée en aucun point de son domaine de définition dans lequel elle est continue.
La fonction donnée par Weierstrass est la suivante:
F(x) =
∞
Σ
n=0
bncos(anπx)
Pour ∣ b ∣ < 1, F(x) est uniformément convergente car absolument convergente, et on établit aisément:
−1
1−b
≤
∞
Σ
n=0
bncos(anπx) ≤
1
1−b
Nous imposerons en plus à a d'être impair et au produit ab, d'être supérieur à 1+3π/2, alors cette fonction n'admet de dérivée en aucun point. On trouvera des démonstrations dans GOUR[1] et DBR[1] qui sont distinctes. Ici nous allons esquisser la démontration de Goursat.
Cette fonction ainsi définie est à peu près impossible à dessiner. Au voisinage de chacun de ses points elle oscille indéfiniment et les oscillations s'écrasent un peu à la manière de x.sin1/x au voisinage de 0.
Nous devons étudier la dérivée: limh → 0F(x+h) − F(x)/h

posons: limh → 0F(x+h) − F(x)/h = Rm + Sm avec

Rm =
1
h
m−1
Σ
n=0
bn[cos(anπ(x+h)) − cos(anπx)]
Sm =
1
h
∞
Σ
n=m
bn[cos(anπ(x+h)) − cos(anπx)]


Le principe de la démonstration consiste à choisir la manière dont h tend vers 0 et mettre en évidence le fait que la tangente à la courbe près de ce point devient verticale (cas de la démonstration de Goursat), ou oscille entre −∞ et +∞ (cas de la démonstration de Du Bois-Reymond).

Majoration de ∣ Rm∣

On utilise la formule des accroissements finis: f(x+h) − f(x) = hf'(c), c ∈ ]x,x+h[ d'où
∣ Rm∣ ≤
1
∣ h∣
m−1
Σ
n=0
∣ bn[−h(−an)π sin( anπ c)]∣ ≤
1
∣ h∣
m−1
Σ
n=0
π bnan∣ h∣ =π
ambm−1
ab−1
Si on suppose ab > 1 on a la majoration désirée: ∣ Rm∣ < π(ab)m/ab−1
On remarque que si ab < 1 la série des dérivées converge uniformément et la fonction F(x) est dérivable.

Minoration de ∣ Sm∣

Décomposons amx en sa partie entière et sa partie décimale:
amx = αm + ξm avec αm=E(amx) et ξm vérifiant: −1/2<ξm≤1/2
On impose à h la façon dont il doit tendre vers 0 en posant:
h = em−ξm/am avec em = ± 1 et donc −3/2≤ em − ξm≤ 3/2, d'où: ∣ h∣ ≤ 3/2am on a donc:
anπ(x+h) = π an−mam(x+h) = π an−m(amx+amh) = π an−m(αm + ξm+em − ξm) = π an−m(αm + em)
Le nombre a étant impair, am est impair, donc an−m est aussi impair et em = ± 1 nous montrent que an−m(αm + em) est de même parité que αm+1, par suite cos(π an−m(x+h)) = (−1)αm+1

De même on a :
cos(anπ x) = cos(π an−mamx) = cos(π an−m(αm + ξm))

cos(anπ x) = cos(π an−mαm).cos(π an−mξm) − sin(π an−mαm).sin(π an−mξm)
mais an−mαm est un entier de même parité que αm puisque an−m est impair, d'où
cos(π an−mαm)=(−1)αm et sin(π an−mαm) = 0 ∀ m .

Ainsi cos(anπ x) = (−1)αm.cos(π an−mξm), d'où
Sm =
1
h
∞
Σ
n=m
bn[cos(anπ(x+h)) − cos(anπx)]
Sm =
1
h
∞
Σ
n=m
bn[(−1)αm+1 − (−1)αmcos(π an−mξm)]
Sm =
1
h
∞
Σ
n=m
bn[(−1)αm+1 − (−1)(−1)αm+1cos(π an−mξm)]
Sm =
(−1)αm+1
h
∞
Σ
n=m
bn[1+cos(π an−mξm)]
Tous les termes de la série étant positifs, la somme est supérieure à son premier terme, d'où
∣ Sm∣ > bm/∣ h∣, mais ∣ h∣ = ∣ em − ξm∣/am,d'où ∣ h∣ < 3/2am et 1/h > 2am/3 ⇒ ∣ Sm∣ > 2ambm/3

Suposons que l'on ait: 2ambm/3 > π(ab)m/ab−1 ce qui donne ab−1 > 3π/2 soit ab > 1 + 3π/2
et
∣ ∣ Rm∣ − ∣ Sm∣ ∣ ≤ ∣ F(x+h) − F(x)/h∣ ≤ ∣ Rm∣ + ∣ Sm∣
mais comme nous avons choisi ∣ Sm∣ > 2(ab)m/3 > π(ab)m/ab − 1
∣ ∣ Rm∣ − ∣ Sm∣ ∣ = ∣ Sm∣ − ∣ Rm∣

∣ F(x+h) − F(x)/h∣ ≥ ∣ Sm∣ − ∣ Rm∣ > 2(ab)m/3 − π(ab)m/ab − 1

∣ F(x+h) − F(x)/h∣ > 2(ab)m/3[ab − (1 + 3π/2)/ab − 1]
Quand m tend vers l'infini h tend vers 0 car ∣ h ∣ < 3/2am et l'expression 2(ab)m/3[ab − (1 + 3π/2)/ab − 1] tend vers l'infini car ab > 1. Il n'existe pas de dérivée déterminée.

  Les travaux de Dini (1854 - 1918)

Quand Weierstrass eut exhibé cette fonction, les mathématiciens s'étonnent de ces nouvceautés et vont se diviser en deux clans: les mathématiciens qui comme Hermite considèrent ces nouvelles venues comme des anomalies et ceux qui, comme Dini, vont se passionner pour ces questions nouvelles.
Dini généralise le cas particulier de Weierstrass et étudie les conditions que doivent vérifier les séries entières pour converger vers des fonctions continues non dérivables et met ainsi en évidence toute une classe de telles fonctions en examinant comment chaque fonction de la série doit osciller pour conduire aux conditions de non dérivabilité.
Voici ici résumées des conditions à vérifier pour fabriquer des fonctions continues non dérivables.
Considérons une suite de fonctions continues et dérivables sur l'intervalle [a,b] que nous noterons Un(x). Nous allons définir la fonction somme des termes de cette suite:
F(x) =
∞
Σ
n=0
Un(x)
Le calcul de la dérivée de cette fonction nous permet d'écrire:
F(x+h) − F(x)
h
= [
m−1
Σ
n=0
Un(x+h) − Un(x)
h
] +
Um(x+h) − Um(x)
h
+
Rm(x+h) − Rm(x)
h
Où Rm(x) représente le reste de la série.
Les conditions pour que F(x) existe et ne soit dérivable en aucun point de l'intervalle [a,b] sont les suivantes:
  1. la série
    ∞
    Σ
    n=0
    		Un(x)
    est uniformenent convergente.
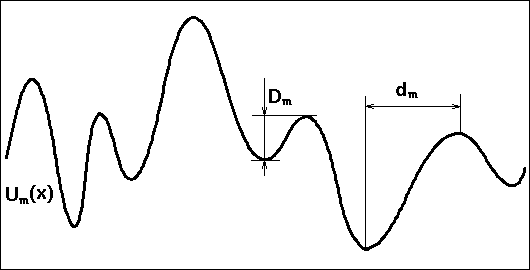
  2. Un(x) a un nombre fini de maxima et de minima dans l'intervalle [a,b] et ce nombre croit indéfiniment avec n.
  3. Les maxima et les minima se succèdent à une distance qui tend vers 0 quand n croit.
  4. on a limm → ∞Dm/dm = 0 avec Dm l'amplitude minimale des oscillations de Um(x) et dm la plus grande distance entre un maximun et et un minimum consécutifs.
  5. on a
    2Rm'
    Dm
    		+
    4dm
    Dm
    m−1
    Σ
    n=o
    		Um' < 1
    pour tout m, avec Rm' = maxx ∈ [a,b](Rm(x+h) − Rm(x)) et Um' = maxx ∈ [a,b](Um'(x))

Exemples

On peut donner un grand nombre d'exemples de telles fonctions:
∞
Σ
n=0
an(cos(bnx))2Pn+1
∞
Σ
n=0
an(sin(bnx))2Pn+1
∞
Σ
n=0
an(cn(bnx))2Pn+1
∞
Σ
n=0
an(sn(bnx))2Pn+1
avec les conditions supplémentaires:
Σn=0∞an converge et an constante
bn tend vers l'infini avec n et anbn ne tendant pas vers 0 avec n et Pn suite d'entiers croissants avec n
sn et cn sont les respectivement les sinus et cosinus elliptiques.
On peut citer d'autres exemples:
∞
Σ
n=1
αncos(1.3.5.7...(2n−1)x)
1.3.5.7...(2n−1)
∞
Σ
n=0
αnsin(1.5.9...(4n+1)x)
1.5.9..(4n+1)
avec ici α >1+3π/2

Citons aussi la fonction de Van Den Warden plus récente dont l'étude est un plus simple que le travail original de Weierstrass, et dont on trouvera le détail dans [CHA] page 140.
∞
Σ
n=0
d(4nx)
4n
avec d(z) représentant l'entier le plus proche de x.

Ces fonctions sont à peu près impossibles à dessiner. Cependant Bolzano a donné un exemple de telle fonction basée sur une suite de fonctions affines par morceaux dont on peut visualiser les étapes et ainsi se faire une idée de l'allure de la fonction. On trouvera cette fonction détaillée dans [CHA] page 141.
Ces fonctions continues sans dérivée ne sont pas exceptionnelles. Banach a montré que dans un certain sens elles sont bien plus nombreuses que les classiques fonctions continues dérivables. De manière un peu plus précise on munit l'espace vectoriel C([a,b]) des fonctions continues sur [a,b] de la norme de la convergence uniforme: ∣∣ f∣∣ = supx ∈ [a,b](∣ f(x)∣), on en fait ainsi un espace vectoriel topologique normé dont on peut montrer qu'il est complet pour cette norme.

On appelle ensemble maigre d'un espace topologique un ensemble obtenu comme union finie de fermés d'intérieur vide. On montre alors que C([a,b]) n'est pas maigre (théorème de Baire) et que l'ensemble des fonctions continues dérivables (sauf peut-être sur ensemble de mesure nul) est un ensemble maigre pour la topologie ci-dessus définie. C'est en ce sens que les fonctions continues sans dérivée sont plus nombreuses que les autres. On trouvera plus de détails la dessus dans [VAP] page 120.

Aspect géométrique

Parallèlement à la notion de fonction continue sans dérivée s'est développé le concept de courbe sans tangente.

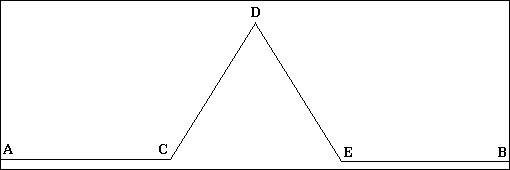
C'est le suédois Helge Von Koch qui donne le premier un exemple de telle courbe. Cette courbe est maintenant devenue classique. Il part d'un segment de droite AB dont il remplace le tiers médian par un triangle équilatéral dont il a enlevé la base. Il obtient ainsi une courbe ACDEB à trois points anguleux. Il recommence cette construction sur chacun des segments AC,CD,DE et EB et ainsi de suite indéfiniment. A la limite on obtient une courbe, qui n'est pas une fonction, et qui ne possède aucune tangente en aucun point, car les points anguleux forment en ensemble dense dans l'ensemble des points de la courbe.

Cette courbe à la particularité de ne pas être rectifiable, c'est-à-dire que sa longueur est infinie. En effet on enlève dans la construction de la courbe un tiers pour le remplacer par deux tiers, ce qui fait qu'à la première étape la longueur de la courbe a été multipliée par 4/3 et qu'à létape n sa longueur a été multipliée par (4/3)n.
Von Koch a modifié sa construction pour rendre rectifiable la courbe. Au lieu d'enlever le tiers médian il enlève un segment de longueur b1 et y place un triangle équilatéral. La courbe a alors une longueur valant l + 2b1 si l est la longueur initiale, et il recommence sur chacun des 4 cotés restants en choisissant un segment de longueur b2. A l'étape n il obtient une courbe de longueur l+2Σi=1n4ibi. Si on choisit bi pour que la série converge, on obtient une courbe de Von Koch rectifiable, seulement Von Koch ne peut plus démontrer qu'elle n'admet aucune tangente. La question de savoir s'il y a équivalence entre courbe sans tangente et courbe non rectifiable est un problème ouvert en 1906 quand Von Koch publie ses travaux.
Il y a un grand nombre de telle courbes dont la plus connue à part celle de Von Koch, est la courbe de Peano qui passe par tous les points d'un carré qui est continue non rectifiable et bien sur sans tangente. Le monde plus récent des courbes fractales donne des exemples très spectaculaires, mais ce n'est plus l'objet de ce petit exposé.

Bibliographie

This document was translated from LATEX by HEVEA.