Mail/M'écrire


Chapitre 3  TERMES INVERSIBLES A GAUCHE OU A DROITE DANS LE LAMBDA CALCUL.

(André Brouty)
Cet exposé est sous licence libre LLDD.
Dans ce chapitre nous nous plaçons dans le système L. Il n'y a donc pas la règle d'extensionalité.

3.1  TERMES INVERSIBLES A GAUCHE.

Une λ-expression X admet un inverse à gauche que nous noterons X−g dans ce paragraphe si et seulement si B X−g X=I, avec B=λ(x0 x1 x2) (x0 (x1 x2)) et I=λ(x)x. Nous utiliserons la représentation des λ-expressions sous forme d'arbres de Bohm. Une remarque d'abord qu'il n'est pas inutile de faire: les arbres de Bohm caractérisent surtout les éléments de Φ(L) c'est-à-dire les approximations directes des éléments de L. Une grande partie de cette étude a donc lieu dans Φ(L). Commençons d'abord par caractériser un sous ensemble particulier de Φ(L).

3.1.1  Extension terminale des arbres de Bohm.

Soient A1 et A2 deux arbres de Bohm d'éléments de Φ(L). Nous dirons que A2 est une extension terminale de A1 relativement à une feuille h étiquetée λ(xi1 xi2 … xik) xt si A2 est obtenu à partir de A1 par l'une et l'une seulement des deux substitutions suivantes:
  1. la feuille h de A1 est devenue dans A2 la feuille h' étiquetée λ(xi1 xi2 … xik xik+1)xt (extension terminale de type 1)
  2. la feuille h est remplacée par l'arbre Ah dont la racine est étiquetée λ(xi1 xi2 … xik) xj et qui possède m fils (m>0) dont un seul est xt, les autres étant Ω; et où xj est une variable liée sur le chemin de la racine de A1 à h distincte de xt (extension terminale de type 2).

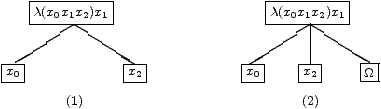
3.1.2  Exemples



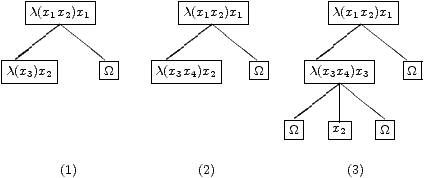
Le passage du premier arbre au deuxième s'est fait par une extension de type 1 et du second au troisième par une extension de type 2. De manière intuitive une extension terminale de type 1 revient à prévoir une variable liée supplémentaire dans une expression et une extension de type 2 à créer cette variable.

On notera A —→t A' pour dire que A' est une extension terminale de A pour une et une seule feuille de A. Remarquons qu'une extension terminale de type 2 pour une feuille h etiquetée λ(xi1… xik) xj est complètement caractérisée par un triplet (xj , m , t) où xj est la variable de tête de h , m le nombre de fils de h dans l'extension et t la position de l'unique fils different de Ω; ainsi dans l'exemple précédent le triplet associé au sommet λ(x3 x4) x3 est (x3 , 3 ,2).
Construisons maintenant de manière inductive l'ensemble suivant noté H:
  1. I est élément de H
  2. Si N est élément de H et si on a AB(N) —→t AB(N') alors N' est aussi élément de H
On ne sera pas surpris d'apprendre que H caractérise un ensemble de termes inversibles. De manière plus précise on a le théorème suivant:
Théorème 1   Un élément X de L a au moins un inverse à gauche si Φ(X) est dans H.
Examinons d'abord un exemple. Pour cela construisons un élément de H et à chaque étape de sa construction donnons un inverse à gauche de la λ-expression associée. Les deux premières étapes de la construction sont imposées. On part de I dont l'inverse à gauche est I.
AB(I) est     λ(x0) x0
Il devient par une extension terminale de type 1
AB(A1)      λ(x0 x1) x0
On n'a pas le choix. (A1 est le célèbre avaleur de variables plus connu sous le nom K). Cherchons un inverse à gauche sous la forme λ(z)(z X1X2… Xp)=Z. On doit avoir B Z A1 x=x, soit B Z A1 x=Z(A1 x)=A1 x X1 X2… Xp=x on voit qu'il suffit de prendre p=1 et alors un inverse à gauche de K est Z=λ(z) (z X1), X1 étant un terme quelconque d'où une infinité d'inverses à gauche pour K.
Poursuivons par une extension de type 1, AB(A1) peut devenir par exemple:
AB(A2)      λ(x0 x1 x2) x0
un calcul analogue montre qu'un inverse possible est Z1=λ(z) (z X1 X2) (deux termes indeterminés). En effet Z1(A2 x)=A2 x X1 X2=x. Continuons maintenant par une extension terminale de type 2, on obtient par exemple AB(A3)

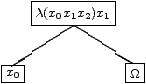
ce qui correspond à
A3=λ(x0 x1 x2) (x1 x0 Ω).
Dans la recherche d'un inverse à gauche de A3 on constate que Z1 où X1 vaut K convient. On l'appellera Z2:
Z2=λ(z) (z K X1)
En effet
Z2(A3 x) = A3 x K X1
  = K x X1
  = x
On a donc particularisé un terme indéterminé dans l'inverse précédent, cela s'explique par le fait qu'on a créé une variable liée qui intervient dans le calcul. Si l'on continue par une extension de type 2 en créant la dernière variable liée qui nous reste on va voir qu'on particularise le terme indéterminé de Z2. Nous obtenons par exemple AB(A4):

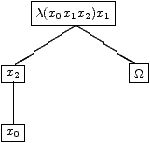
Correspondant à
A4=λ(x0 x1 x2) (x1 (x2 x0) Ω)
Ici un inverse à gauche est Z3=λ(z) (z K I) où on a particularisé le terme indeterminé de Z2. On a
Z3(A4 x) = A4 x K I
  = K (I x) Ω
  = x
Si nous continuons par une extension de type 2 on voit qu'on a épuisé le stock de variables liées disponibles, on ne peut donc le faire qu'en réutilisant une variable dejà mise. Nous obtenons par exemple AB(A5):

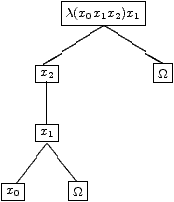
ce qui correspond à
A5=λ(x0 x1 x2) (x1 (x2 (x1 x0 Ω)) Ω)
On constate ici que Z3 est aussi un inverse de A5; en effet
Z3(A5 x) = A5 x K I
  = K (I (K x Ω)) Ω
  = I (K x Ω)
  = K x Ω
  = x
Malheureusement ceci n'est qu'un cas particulier qui se produit parce que le triplet caractérisant les extensions de type 2 associé à la variable de tête x1 est le même pour toutes les occurrences de cette variable en position de tête.
Il en serait tout autrement si nous avions fait une extension de type 2 relativement à x1 avec deux triplets distincts, par exemple AB(A6)

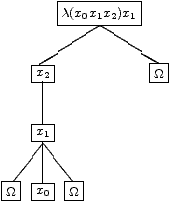
Ceci nous conduit à poser deux définitions: Ainsi l'arbre représentant A6 n'est pas homogène car il y a deux occurrences de x1 qui ont comme triplet (x1,2,1) et (x1,3,2). Pour trouver un inverse à gauche dans une telle situation on va modifier la λ-expression de manière à la rendre homogène en faisant en sorte qu'un inverse de l'expression obtenue permette d'obtenir aisément un inverse de l'expression de départ. Soit donc B6 la λ-expression obtenue à partir de A6 en éliminant (dans A6) l'abstraction de x1 (variable qui fait que l'arbre associé à A6 n'est pas homogène) et en substituant chaque occurrence de la variable x1 par la λ-expression
P3=λ(t0 t1 t2 t3) (t3 t0 t1 t2).
On obtient:
λ(x0 x2) (P3(x2(P3 Ω x0 Ω))Ω)
soit après réduction
λ(x0 x2 t2 t3) (t3(x2(λ(t3) (t3 Ω x0 Ω)))Ω t2)
ou encore pour éviter toute confusion entre variables:
B6=λ(x0 x2 t2 t3) (t3(x2(λ(t4) (t4 Ω x0 Ω)))Ω t2)
dont l'arbre de Bohm associé est:

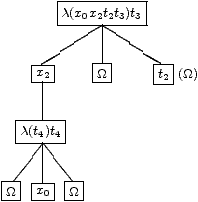
Un tel objet n'est pas dans H puisque la variable t2 a été intoduite et occupe la position d'une feuille. Cela provient du fait que dans l'arbre associé à A6 la première occurrence de la variable x1 n'a pas le même nombre de fils que la seconde. On se ramène à un élément de H en remplaçant toute feuille distincte de x0 par Ω. Nous l'avons fait figurer entre parenthèses sur le schéma. Nous obtenons ainsi un élément de H homogène, B'6, dont nous pouvons calculer un inverse. Nous affirmons qu'un inverse de B'6 que nous appelerons Z6 nous permet d'obtenir un inverse à gauche de A6. En effet Z6 est aussi, par construction, un inverse à gauche de B6. Il a la forme
Z6=λ(z) (z U1 U2 … Un)
alors
Z'6=λ(z) (z P3 U1 U2... Un)
est un inverse à gauche de A6 puisque
B6 y = A6 y P3
Z6(B6 y)=y
Z6(B6 y)=Z6(A6 y P3)=Z'6(A6 y).
A titre d'exemple cherchons donc maintenant cet inverse pour B'6. Pour cela, de même, construisons B'6 à partir des différentes extensions et donnons à chaque étape de la construction un inverse à gauche correspondant. Précisons d'abord que dans ce qui suit Xi désigne un terme quelconque de L.
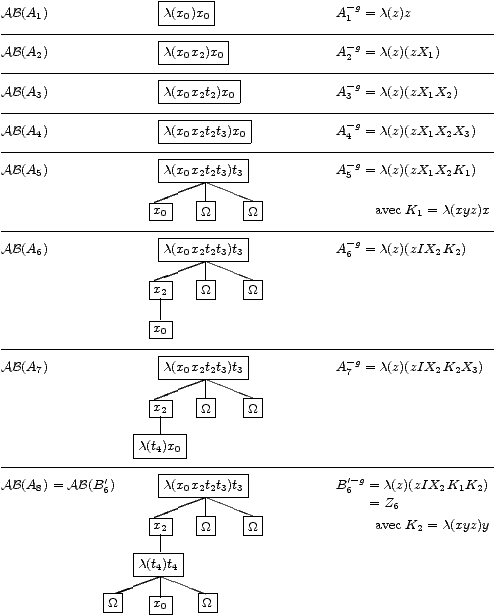Nous avons donc Z6=λ(z) (z I X2 K2 K1) qui est un inverse à gauche de B'6 ainsi que de B6. Nous sommes donc en mesure de donner maintenant un inverse à gauche de A6, l'expression non homogène qui nous intéresse. Cet inverse est
Z6−g=λ(z) (z P3 I X2 K2 K1).
On peut faire une vérification directe de ce résultat. On a:
A6=λ(x0 x1 x2) (x1(x2(x1 Ω x0 Ω))Ω)
P3=λ(t0 t1 t2 t3) (t3 t0 t1 t2)
donc
B Z6−g A6 y = Z5−g(A6 y)
  = A6 y P3 I X2 K1 K2
  = P3(I(P3 Ω y Ω))Ω X2 K1 K2
  = K2(I(P3 Ω y Ω))Ω X2 K2
  = I(P3 Ω y Ω)K2
  = P3 Ω y Ω K2
  = K2 Ω y Ω
  = y

3.1.3  Généralisation et démonstration du théorème

A la lumière de l'exemple ci-dessus detaillé, il est maintenant possible d'exposer sans entrer dans un détail de présentation fastidieux les grandes lignes de la démonstration du théorème précédent.

On remarque d'abord qu'il n'y a qu'une seule façon de construire un élément de H à partir des extensions terminales de type 1 ou 2. La démonstration se fait donc par récurrence sur le nombre d'étapes de cette construction. Soit donc H un élément de L tel que Φ(H) est dans H. Le départ de cette construction est H0=I=λ(x0) x0 dont on connait bien un inverse à gauche qui est lui-même. On suppose donc (hypothèse de récurrence) qu'à l'étape k de cette construction on a obtenu l'expression Hk dont on connait un inverse à gauche, noté Hk−g, et qui a la forme:
Hk−g=λ(z) (z X1 X2… Xp).
L'expression Hk+1 est obtenue à partir de Hk par une extension terminale de type 1 ou une extension terminale de type 2.

1er cas

Hk+1 est obtenu à partir de Hk par une extension terminale de type 1. Il suffit alors d'ajouter un terme quelconque à Hk−g pour obtenir Hk+1−g:
Hk+1−g=λ(z) (z X1 X2… Xp Xp+1).
En effet on a:
Hk+1 y = S(Hk y)[y ←— λ(t) y]
Hk−g(Hk+1 y)=Hk+1 y X1… Xp
=λ(t) y par hypothèse de récurrence
et ainsi
Hk+1−g(Hk+1 y)=λ(t) y Xp+1=y

2eme cas

Hk+1 est obtenu à partir de Hk par une extension terminale de type 2. Ici il y a deux sous cas:
  1. L'arbre associé à Hk+1 est homogène. Soit (xj,m,q) le triplet associé à la variable xj introduite lors de cette extension; alors si xj a dejà une autre occurrence dans l'arbre par hypothèse d'homogénéité les triplets associés à xj sont les mêmes et on a Hk+1−g=Hk−g. Autrement si xj ne possède pas d'autre occurrence Hk+1−g est obtenu à partir de Hk−g en particularisant le sous terme Xj de Hk−g qui ne jouait aucun rôle jusqu'ici puisqu'il ne lui correspondait aucune variable. De manière plus précise on a:
    Hk+1−g=λ(z) (z X1 X2… Xj−1 U[q,m] Xj+1… Xp)
    avec
    U[q,m]=λ(t1… tm) tq
    En effet on a dans le cas d'une telle extension:
    Hk+1 y = S(Hk y)[y ←— xj V1 V2… Vq−1 y Vq+1… Vm]
    où les Vi sont des termes de L non résolubles, alors
    Hk+1−g(Hk+1 y) = Hk+1 y X1 … Xj−1 U[q,m] Xj+1 … Xp
      = U[q,m] V1 V2 … Vq−1 y Vq+1 … Vm
      = y
  2. L'arbre n'est pas homogène pour une variable xj
    Cela signifie qu'il y a plusieurs variables xj pour lesquelles sont associés des triplets (xj,m1,k1) ...(xj,mr,kr) dont deux au moins sont distincts. Alors on fabrique l'expression F obtenue à partir de Hk+1 par suppression de l'abstraction de xj et en substituant chaque occurrence de xj par le permutateur
    Pm=λ(t0 t1 … tm) (tm t0 t1 … tm−1)
    avec
    m=max{m1,m2 … mr}
    Or comme on l'a vu dans l'exemple précédent F n'est plus dans H; on s'y ramène en construisant F1 obtenue en remplaçant dans F chaque feuille distincte de x0 par Ω. D'après 1 on sait construire un inverse à gauche de F1 que nous appellerons F−g. Par construction F−g est également un inverse à gauche de F. On a donc
    F−g=λ(z) (z Z1 Z2 … Zp)
    et on obtient un inverse de Hk+1 en posant:
    Hk+1−g=λ(z) (z Z1 Z2 … Zj−1 Pm Zj Zj+1 … Zp)
    on a ainsi
    F y Z1 Z2 … Zj−1=Hk+1 y Z1 Z2 … Zj−1 Pm
    donc
    Hk+1−g(Hk+1 y) = Hk+1 y Z1 Z2 … Zj−1 Pm Zj … Zp
      = F y Z1 Z2 … Zj−1 Zj … Zp
      = F−g(F y)
      = y
    Maintenant il est clair que ce mécanisme de recherche peut être aisément généralisé au cas où l'expression Hk+1 a une approximation directe dans H non homogène pour plusieurs variables.
Il est possible d'être un peu plus précis en montrant que chaque élément H de L dont l'approximation directe Φ(H) est dans H possède une infinité d'inverses à gauche non équivalents si H est distinct de I=λ(x) x.
En effet si Φ(H) est obtenu uniquement à partir d'extensions terminales de type 1 alors un inverse à gauche a la forme
H−g=λ(z) (z X1 X2 … Xp)
où Xi représente un terme quelconque; le résultat est alors clair. Si maintenant Φ(H) a été obtenu en faisant au moins une extension terminale de type 2 alors il y a nécessairement dans H−g un sous terme Xi qui est le projecteur U[k,m]=λ(t1 t2 … tm) tk et ainsi
H−g=λ(z) (z X1 … Xi−1 U[k,m] Xi+1 … Xp)
alors
H1−g=λ(z) (z X1 … Xi−1 U[k,m+n] Xi+1 … Xp Y1 … Yn)
où les Yj sont des termes quelconques de L est aussi un inverse à gauche de H. Ici aussi le résultat est maintenant clair.

3.1.4  Caractérisation des termes inversibles à gauche

Soit X un élément de L, introduisons l'ensemble suivant:
A(X)={M | M ∈ Φ(L) et M<Φ(X)}
et posons
H(X)= A(X)∩ H.
On a alors le théorème suivant:
Théorème 2   Un élément X de L admet au moins un inverse à gauche si et seulement si H(X)≠Ø.
Dans le calcul de la vérification de l'inverse à gauche d'un terme X on s'aperçoit que dans l'arbre de Bohm représentant X tous les sommets étiquetés Ω sont amenés à disparaitre. On peut donc remplacer ces sommets par n'importe quelle λ-expression sans changer l'inverse dejà trouvé. C'est cela l'idée de la caractérisation des termes inversibles à gauche de L.

Si H(X) n'est pas vide il contient un élément X1 de H dont on sait trouver un inverse à gauche. Par définition de la relation d'ordre dont est muni Φ(L) (voir chapitre 1 paragraphe 13). X est obtenu à partir de X1 en remplaçant dans X1 certaines feuilles étiquetées Ω par des λ-expressions particulières et ainsi l'inverse à gauche de X1 déterminé par la stratégie précédente est aussi un inverse à gauche de X, ce qui établit la condition suffisante du théorème.

Avant d'aborder la condition nécessaire examinons un petit exemple. Soit
X=λ(x0 x1 x2) (x1(λ(x3) (x3(x0 x0)x5)(λ(x4) (x4 O x0))x0).
Rappelons que O=λ(x) (x x) λ(x) (x x) est une expression non résoluble bien connue. H(X) est-il vide? Non car l'expression X1 suivante vérifie X1 < Φ(X).
X1=λ(x0 x1 x2) (x1 Ω λ(x4) (x4 Ω x0) Ω)
Donnons les arbres de Bohm associés.

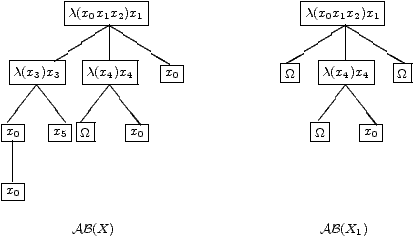
On voit plus clairement sur ces schémas quels sommets étiquetés Ω ont été remplacés dans X1 par des termes pour l'obtention de X. Ainsi l'inverse à gauche de X1 calculé comme précédemment sera un inverse à gauche de X. On remarque que X contient une variable libre. Quelles sont donc maintenant les conditions nécessaires pour qu'une telle situation se produise, c'est-à-dire pour que H(X) ne soit pas vide ? Une λ-expression qui impose H(X) non vide est telle qu'il existe dans AB(X) au moins une feuille w telle que
  1. x0 est l'étiquette de w et x0 ne figure pas comme variable de tête sur le chemin de la racine à w.
  2. chaque variable de tête sur le chemin de la racine à w est liée.
Il est maintenant facile d'établir la condition nécessaire du théorème. Cela se fait par l'absurde. Supposons donc que H(X) soit vide et montrons qu'alors il n'est pas possible de trouver un inverse à gauche à X. En effet il nous faut alors nier les conditions 1 et 2 ci-dessus. Ainsi pour toute feuille w de AB(X) x0 n'apparait pas comme étiquette de w; soit x0 n'apparait nulle part alors (X y) ne contient pas y et il sera évidemment impossible de trouver X−g tel que X−g(X y)=y.
Soit x0 apparait mais pas comme étiquette de w alors dans (X y) la variable y va s'appliquer à d'autres variables ce qui ne doit pas être. Ou bien pour toute feuille w il y a un sommet non terminal de l'arbre qui contient une variable libre, alors il n'existe pas d'expression X−g telle que X−g(X y) fasse disparaitre la variable libre sans faire disparaitre y. Le théorème est demontré.

Pour terminer ce paragraphe donnons quelques exemples simples de λ-expressions n'admettant pas d'inverse à gauche dans L. Les expressions bien connues:
Bλ=λ(x0 x1 x2) (x0(x1 x2))
Cλ=λ(x0 x1 x2) (x0 x2 x1)
Sλ=λ(x0 x1 x2) (x0 x2(x1 x2))
n'admettent pas d'inverse à gauche dans L car leurs arbres de Bohm ne vérifient pas les conditions 1 et 2 ci-dessus.

3.2  TERMES INVERSIBLES A DROITE.

De manière analogue nous dirons qu'un terme X de L admet un inverse à droite que nous noterons X−d si B X X−d=I.

Nous allons de même d'abord introduire un type d'extension des arbres de Bohm.

3.2.1  Extension initiale des arbres de Bohm

Soient A1 et A2 deux arbres de Bohm. Nous dirons que A1 est une extension initiale de A2 si A2 est obtenu à partir de A1 en ajoutant la feuille Ω à la racine de A1 en ajoutant une branche à droite de A1. On notera A1 —→i A2 une telle extension.

Exemple


Construisons de manière inductive l'ensemble R suivant: Il est facile de décrire l'ensemble R ainsi obtenu:
R={λ(x) x,λ(x) (x Ω),λ(x) (x Ω Ω),λ(x) (x Ω Ω Ω) ……}
Cet ensemble n'est évidemment pas très riche c'est pourquoi on a le théorème précis suivant:
Théorème 3   Soit X un élément de L tel que Φ(X) est dans R, alors X possède un et un seul inverse à droite.

Existence

Le projecteur X−d=λ(x0 x1 … xn) x0 est un inverse à droite de
Φ(X)=λ(x)(x Ω Ω … Ωn fois)
élément de R, et donc aussi un inverse de X. En effet X s'écrit X=λ(x) (x X1 X2 … Xn) où les Xi sont des termes non résolubles et
X(X−d y)=X−d y X1 X2 … Xn=y

Unicité

Pour cela supposons l'existence d'un autre inverse à droite de X que nous noterons X1−d.
X1−d=λ(x0 x1 … xh) (xj Y1 Y2 … Yq)
on a
X(X1−d y)=X1d y X1 X2 … Xn=y.
Nécessairement h≤ n autrement il resterait des abstractions qu'on ne pourrait pas éliminer. De plus X1−d a un inverse à gauche qui est X. D'après le premier paragraphe H(X) n'est pas vide donc

si q=0 alors X1−d=λ(x0 x1 … xh) x0 par propriété des termes inversibles à gauche et X1−d=X−d.

Si q≠ 0 alors xj≠ x0 toujours par propriété des termes inversibles à gauche on a donc
X(X1−d y) = X1−d y X1 X2 … Xn
  = Xj Y1' Y2' … Yq' Xq+1 … Xn
  = y
avec
Yi'= S(Yi)[x0 ←— y,x1 ←— X1, … ,xh ←— Xh] et 1≤ i ≤ q
et ceci est évidemment absurde puisque Xj n'est pas résoluble.

3.2.2  Caractérisation des termes inversibles à droite

Soit X un terme de L; introduisons l'ensemble
R(X)= A(X)∩ R
On a alors le théorème suivant:
Théorème 4   Un terme X de L admet au moins un inverse à droite si et seulement si R(X) n'est pas vide.
Ici l'idée est la même que pour les termes inversibles à gauche: les sommets d'un élément V de R étiquetés Ω peuvent être remplacés par n'importe quelle expression pour donner un terme qui admettra comme inverse à droite un inverse à droite de V. Par exemple le terme X dont l'arbre de Bohm est:
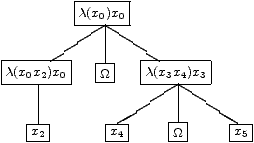
a une approximation directe supérieure pour l'ordre choisi à la λ-expression λ(x0) (x0 Ω Ω Ω) qui est dans R et ainsi un inverse à droite de cette dernière expression qui est λ(x0 x1 x2 x3) x0 est aussi un inverse à droite de X; ce qui établit la condition suffisante du théorème.

Pour établir la condition nécessaire on raisonne par l'absurde et on suppose que R(X) est vide, alors:

soit X a plus d'une abstraction, par exemple X=λ(x0 x1 … xn) xi X1 … Xp alors il y a n abstractions qui ne pourront être éliminées lors du calcul de X(X−d y).

Soit la variable de tête de X est libre et son élimination devient impossible lors du même calcul.

Il suit de tout ceci que dans le contexte où nous sommes placés le seul terme de L ayant à la fois un inverse à droite et à gauche est I=λ(x) x. En effet soit I1 un terme inversible dans (L B I) alors il est inversible à droite et doit avoir la forme λ(x0) (x0 V1 V2 … Vn) où Vi sont des termes de L; mais il est aussi inversible à gauche, son arbre de Bohm doit posséder une feuille étiquetée x0 et qui ne figure que dans cette position sur le chemin de la racine à x0. Comme x0 figure en tant que variable de tête de la racine cela n'est possible que si I1 est λ(x0) x0 d'où le résultat.

Pour terminer ce chapitre il est possible de donner un résultat plus fort concernant l'inversibilité à droite mais portant sur un ensemble de termes plus réduit. Donnons d'abord une définition.
Une λ-expression X est dite être de type Ω (Ω-like) si X n'est pas résoluble ou bien si X est résoluble mais sa variable de tête est libre.
On a alors le résultat suivant:
Théorème 5   Soit X un élément de L tel que R(X) n'est pas vide. X est donc de la forme λ(x) (x X1 X2 … Xn). Si de plus chaque Xi est de type Ω alors X possède un et un seul inverse à droite sinon il en possède une infinité.
En effet si chaque Xi n'est pas résoluble alors Φ(X) est élément de R et on se trouve dans la situation du premier théorème de ce paragraphe. Si maintenant il y a des Xi résolubles avec une variable de tête libre, alors si nous supposons l'existence d'un autre inverse à droite X1−d; celui-ci doit avoir la forme X1−d=λ(x0 x1 … xh) (xj Y1 … Yp) et comme il est inversible à gauche xj doit être différent de x0, alors lors du calcul de X(X1−dy)=X1−d y X1 X2 … Xn on aura à calculer Xj Z1 Z2 … Zk pour des termes Zi et on devra obtenir y or cela n'est pas possible si la variable de tête de Xj est libre et distincte de y.

Supposons maintenant l'existence d'un terme Xi non de type Ω alors Xi est résoluble et il existe q termes Z1 Z2 … Zq tels que Xi Z1 Z2 … Zq=I (voir chapitre 1 paragraphe 11) et ainsi le terme
V=λ(x0 x1 … xn) (xi Z1 Z2 … Zq x0)
vérifie
X(V y) = V y X1 X2 … Xn
  = Xi Z1 Z2 … Zq y
  = y
Également
W=λ(x0 x1 … xn) (xi Z1 … Zq xi Z1 … Zq x0)
est tel que
X(W y)=y
On voit maintenant clairement comment construire une infinité d'inverses à droite de X dans une telle situation.

Pour terminer ce paragraphe on peut donner un petit exemple. Cependant on ne sera pas surpris de constater que les termes inversibles à droite ainsi caracterisés ont la même forme que les inverses à gauche du paragraphe précédent, et pour cause.

Un terme inversible à droite à la forme λ(x) (x X1 … Xp) où les Xi sont des termes quelconques c'est-à-dire qu'il a une seule abstraction de tête; ce qui limite la recherche d'exemples intéressants. Donnons cependant un inverse à droite du célèbre point-fixeur Y qui a précisément cette forme:
Y=λ(f) (f(λ(x) (f(x x)) λ(x) (f(x x))))
et K=λ(x0 x1) x0 est un inverse à droite de Y car Y(K y)=K y(Y(K y))=y.

Algorithme de reconnaissance des combinateurs inversibles